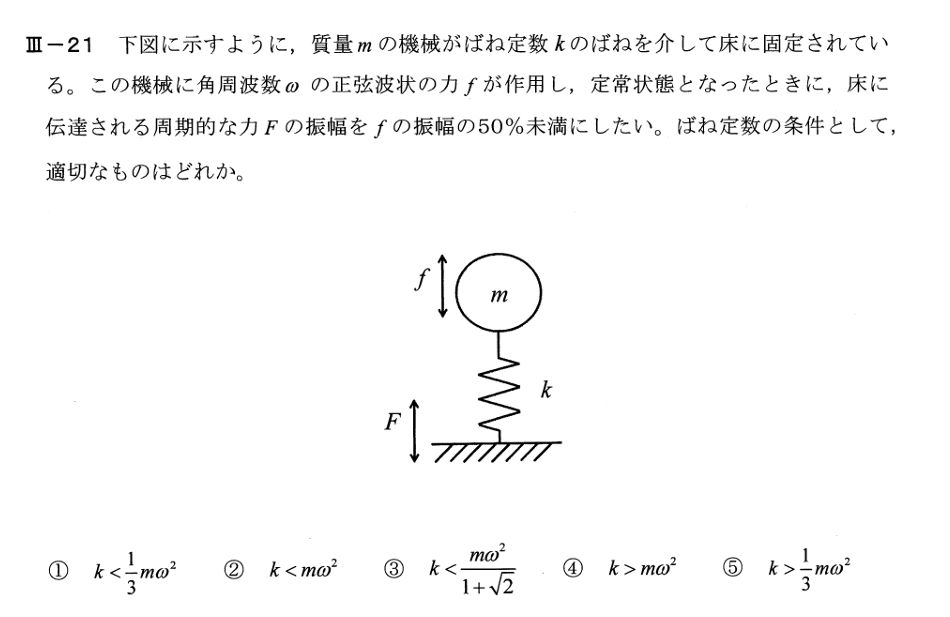
【ChatGPT4 2024.3.17】令和3年度技術士第一次試験問題［機械部門］専門科目Ⅲ-21 機械の床に伝達される振幅

修正した計算によれば、最初の平衡条件からバネ定数 $k$ は $\frac{gm}{x}$ となります。ここで $x$ は質量 $m$ が重力 $g$ のもとでバネを圧縮した初期の圧縮量です。

さらに、初期の圧縮量の半分だけバネを圧縮すると、バネ定数 $k$ は変わらず、新しい圧縮量 $x’ = \frac{3x}{2}$ で $\frac{3mg}{2}$ の力を支える必要があります。

各選択肢を $k = \frac{gm}{x}$ で評価した結果、以下のようになりました：

1. $\frac{1}{x} < \frac{1}{3}$ （つまり $k < \frac{1}{3} m g^2$ ）
2. $\frac{1}{x} < 1$ （つまり $k < m g^2$ ）
3. $\frac{1}{x} < \frac{1}{1 + \sqrt{2}}$ （つまり $k < \frac{m g^2}{1 + \sqrt{2}}$ ）
4. $\frac{1}{x} > 1$ （つまり $k > m g^2$ ）
5. $\frac{1}{x} > \frac{1}{3}$ （つまり $k > \frac{1}{3} m g^2$ ）

ここで $x$ はバネの初期の圧縮量を表す正の値ですので、 $k$ は特定の値より小さいという不等式になります。従って、正解は $k$ が $m g^2$ 未満であるという条件に最も適合する選択肢です。

与えられた選択肢から、 $k > m g^2$ という選択肢は、質量の重さより少ない力でバネをさらに圧縮する必要があるため、不正解です。

残りの不等式から、最も制約が厳しく、 $m g^2$ を超えない最大の境界を示す選択肢を考える必要があります。選択肢 3 の $k < \frac{m g^2}{1 + \sqrt{2}}$ は、 $1 + \sqrt{2}$ が1より大きいため、分母が大きくなり分数が $m g^2$ より小さくなります。